Boyer-Myrvold Planarity Testing/Embedding

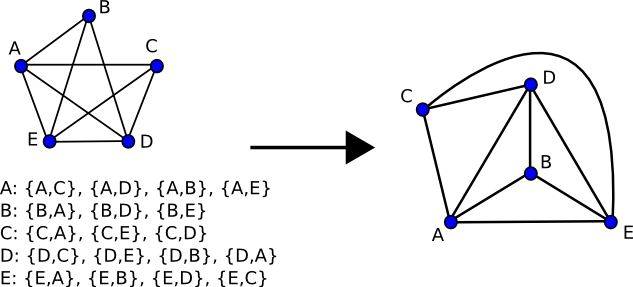
A graph is planar if it can be drawn in two-dimensional space without any of its edges crossing. Such a drawing of a planar graph is called a plane drawing. Each plane drawing belongs to an equivalence class called a planar embedding [1] that is defined by the clockwise ordering of adjacent edges around each vertex in the graph. A planar embedding is a convenient intermediate representation of an actual drawing of a planar graph, and many planar graph drawing algorithms are formulated as functions mapping a planar embedding to a plane drawing.

A planar graph (top left), along with a planar embedding of that graph (bottom left) can be used to create a plane drawing (right) by embedding edges around each vertex in the order in which they appear in the planar embedding.

The function boyer_myrvold_planarity_test implements the planarity testing/embedding algorithm of Boyer and Myrvold [70]. boyer_myrvold_planarity_test returns true if the input graph is planar and false otherwise. As a side-effect of this test, a planar embedding can be constructed if the graph is planar or a minimal set of edges that form a Kuratowski subgraph can be found if the graph is not planar. boyer_myrvold_planarity_test uses named parameter arguments (courtesy of the Boost.Parameter library) to specify what the function actually does. Some examples are:

Testing whether or not a graph is planar:

bool is_planar = boyer_myrvold_planarity_test(g);

Computing a planar embedding for a graph if it is planar, otherwise finding a set of edges that forms an obstructing Kuratowski subgraph:

if (boyer_myrvold_planarity_test(boyer_myrvold_params::graph = g, 
                                 boyer_myrvold_params::embedding = embedding_pmap,  
                                 boyer_myrvold_params::kuratowski_subgraph = out_itr
                                 )
    )
{
  //do something with the embedding in embedding_pmap
}
else
{
  //do something with the kuratowski subgraph output to out_itr
}

The parameters passed to boyer_myrvold_planarity_test in the examples above do more than just carry the data structures used for input and output - the algorithm is optimized at compile time based on which parameters are present. A complete list of parameters accepted and their interactions are described below.

boyer_myrvold_planarity_test accepts as input any undirected graph, even those with self-loops and multiple edges. However, many planar graph drawing algorithms make additional restrictions on the structure of the input graph - for example, requiring that the input graph is connected, biconnected, or even maximal planar (triangulated.) Fortunately, any planar graph on n vertices that lacks one of these properties can be augmented with additional edges so that it satisfies that property in O(n) time - the functions make_connected, make_biconnected_planar, and make_maximal_planar exist for this purpose. If the graph drawing algorithm you're using requires, say, a biconnected graph, then you must make your input graph biconnected before passing it into boyer_myrvold_planarity_test so that the computed planar embedding includes these additional edges. This may require more than one call to boyer_myrvold_planarity_test depending on the structure of the graph you begin with, since both make_biconnected_planar and make_maximal_planar require a planar embedding of the existing graph as an input parameter.

The named parameters accepted by boyer_myrvold_planarity_test are:

graph : The input graph - this is the only required parameter.
vertex_index_map : A mapping from vertices of the input graph to indexes in the range [0..num_vertices(g)). If this parameter is not provided, the vertex index map is assumed to be available as an interior property of the graph, accessible by calling get(vertex_index, g).
edge_index_map: A mapping from the edges of the input graph to indexes in the range [0..num_edges(g)). This parameter is only needed if the kuratowski_subgraph argument is provided. If the kuratowski_subgraph argument is provided and this parameter is not provided, the EdgeIndexMap is assumed to be available as an interior property accessible by calling get(edge_index, g).
embedding : If the graph is planar, this will be populated with a mapping from vertices to the clockwise order of neighbors in the planar embedding.
kuratowski_subgraph : If the graph is not planar, a minimal set of edges that form the obstructing Kuratowski subgraph will be written to this iterator.

These named parameters all belong to the namespace boyer_myrvold_params. See below for more information on the concepts required for these arguments.

Verifying the output

Whether or not the input graph is planar, boyer_myrvold_planarity_test can produce a certificate that can be automatically checked to verify that the function is working properly.

If the graph is planar, a planar embedding can be produced. The planar embedding can be verified by passing it to a plane drawing routine (such as chrobak_payne_straight_line_drawing) and using the function is_straight_line_drawing to verify that the resulting graph is planar.

If the graph is not planar, a set of edges that forms a Kuratowski subgraph in the original graph can be produced. This set of edges can be passed to the function is_kuratowski_subgraph to verify that they can be contracted into a K₅ or K_3,3. boyer_myrvold_planarity_test chooses the set of edges forming the Kuratowski subgraph in such a way that the contraction to a K₅ or K_3,3 can be done by a simple deterministic process which is described in the documentation to is_kuratowski_subgraph.

Where Defined

boost/graph/boyer_myrvold_planar_test.hpp

Parameters

IN: Graph& g

Any undirected graph. The graph type must be a model of VertexAndEdgeListGraph and IncidenceGraph.

OUT PlanarEmbedding embedding

Must model the PlanarEmbedding concept.

IN OutputIterator kuratowski_subgraph

An OutputIterator which accepts values of the type graph_traits<Graph>::edge_descriptor

IN VertexIndexMap vm

A Readable Property Map that maps vertices from g to distinct integers in the range [0, num_vertices(g) )
Default: get(vertex_index,g)

IN EdgeIndexMap em

A Readable Property Map that maps edges from g to distinct integers in the range [0, num_edges(g) )
Default: get(edge_index,g), but this parameter is only used if the kuratowski_subgraph_iterator is provided.

Complexity

Assuming that both the vertex index and edge index supplied take time O(1) to return an index and there are O(n) total self-loops and parallel edges in the graph, most combinations of arguments given to boyer_myrvold_planarity_test result in an algorithm that runs in time O(n) for a graph with n vertices and m edges. The only exception is when Kuratowski subgraph isolation is requested for a dense graph (a graph with n = o(m)) - the running time will be O(n+m) [2].

Examples

Notes

[1] A planar embedding is also called a combinatorial embedding.

[2] The algorithm can still be made to run in time O(n) for this case, if needed. Euler's formula implies that a planar graph with n vertices can have no more than 3n - 6 edges, which means that any non-planar graph on n vertices has a subgraph of only 3n - 5 edges that contains a Kuratowski subgraph. So, if you need to find a Kuratowski subgraph of a graph with more than 3n - 5 edges in time O(n), you can create a subgraph of the original graph consisting of any arbitrary 3n - 5 edges and pass that graph to boyer_myrvold_planarity_test.