 |

The heart of the Boost Graph Library (BGL) is the interface, or concepts (in the parlance of generic programming), that define how a graph can be examined and manipulated in a data-structure neutral fashion. In fact, the BGL interface need not even be implemented using a data-structure, as for some problems it is easier or more efficient to define a graph implicitly based on some functions.
The BGL interface does not appear as a single graph concept. Instead it is factored into much smaller pieces. The reason for this is that the purpose of a concept is to summarize the requirements for particular algorithms. Any one algorithm does not need every kind of graph operation, typically only a small subset. Furthermore, there are many graph data-structures that can not provide efficient implementations of all the operations, but provide highly efficient implementations of the operations necessary for a particular algorithm. By factoring the graph interface into many smaller concepts we provide the graph algorithm writer with a good selection from which to choose the concept that is the closest match for their algorithm. Note that because of the use of traits classes rather than member types, it is not safe (and often will not work) to define subclasses of BGL graph types; those types may be missing important traits and properties that were defined externally to the class definition.
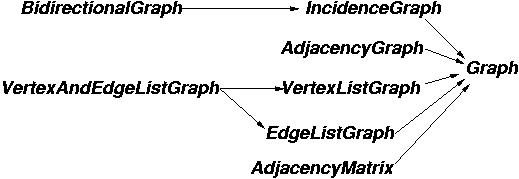
Figure 1 shows the refinements relations between the graph concepts. The reason for factoring the graph interface into so many concepts is to encourage algorithm interfaces to require and use only the minimum interface of a graph, thereby increasing the reusability of the algorithm.
Table 1 gives a summary of the valid expressions and associated types for the graph concepts and provides links to the detailed descriptions of each of the concepts. The notation used in the table is as follows.| G | A type that is a model of Graph. |
| g | An object of type G. |
| e | An object of type boost::graph_traits<G>::edge_descriptor. |
| e_iter | An object of type boost::graph_traits<G>::out_edge_iterator. |
| u,v | Are objects of type boost::graph_traits<G>::vertex_descriptor. |
| ep | is an object of type G::edge_property_type |
| vp | is an object of type G::vertex_property_type |
| Property | A type used to specify a vertex or edge property. |
| property | An object of type Property. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The interface that the BGL provides for accessing and manipulating an undirected graph is the same as the interface for directed graphs described in the following sections, however there are some differences in the behaviour and semantics. For example, in a directed graph we can talk about out-edges and in-edges of a vertex. In an undirected graph there is no ``in'' and ``out'', there are just edges incident to a vertex. Nevertheless, in the BGL we still use the out_edges() function (or in_edges()) to access the incident edges in an undirected graph. Similarly, an undirected edge has no ``source'' and ``target'' but merely an unordered pair of vertices, but in the BGL we still use source() and target() to access these vertices. The reason the BGL does not provide a separate interface for undirected graphs is that many algorithms on directed graphs also work on undirected graphs, and it would be inconvenient to have to duplicate the algorithms just because of an interface difference. When using undirected graphs just mentally disregard the directionality in the function names. The example below demonstrates using the out_edges(), source(), and target() with an undirected graph. The source code for this example and the following one can be found in examples/undirected.cpp.
const int V = 2;
typedef ... UndirectedGraph;
UndirectedGraph undigraph(V);
std::cout << "the edges incident to v: ";
boost::graph_traits<UndirectedGraph>::out_edge_iterator e, e_end;
boost::graph_traits<UndirectedGraph>::vertex_descriptor
s = vertex(0, undigraph);
for (tie(e, e_end) = out_edges(s, undigraph); e != e_end; ++e)
std::cout << "(" << source(*e, undigraph)
<< "," << target(*e, undigraph) << ")" << endl;
Even though the interface is the same for undirected graphs, there are some behavioral differences because edge equality is defined differently. In a directed graph, edge (u,v) is never equal to edge (v,u), but in an undirected graph they may be equal. If the undirected graph is a multigraph then (u,v) and (v,u) might be parallel edges. If the graph is not a multigraph then (u,v) and (v,u) must be the same edge.
In the example below the edge equality test will return false for the directed graph and true for the undirected graph. The difference also affects the meaning of add_edge(). In the example below, if we had also written add_edge(v, u, undigraph), this would have added a parallel edge between u and v (provided the graph type allows parallel edges). The difference in edge equality also affects the association of edge properties. In the directed graph, the edges (u,v) and (v,u) can have distinct weight values, whereas in the undirected graph the weight of (u,v) is the same as the weight of (v,u) since they are the same edge.
typedef ... DirectedGraph;
DirectedGraph digraph(V);
{
boost::graph_traits<DirectedGraph>::vertex_descriptor u, v;
u = vertex(0, digraph);
v = vertex(1, digraph);
add_edge(digraph, u, v, Weight(1.2));
add_edge(digraph, v, u, Weight(2.4));
boost::graph_traits<DirectedGraph>::edge_descriptor e1, e2;
bool found;
tie(e1, found) = edge(u, v, digraph);
tie(e2, found) = edge(v, u, digraph);
std::cout << "in a directed graph is ";
std::cout << "(u,v) == (v,u) ? " << (e1 == e2) << std::endl;
property_map<DirectedGraph, edge_weight_t>::type
weight = get(edge_weight, digraph);
cout << "weight[(u,v)] = " << get(weight, e1) << endl;
cout << "weight[(v,u)] = " << get(weight, e2) << endl;
}
{
boost::graph_traits<UndirectedGraph>::vertex_descriptor u, v;
u = vertex(0, undigraph);
v = vertex(1, undigraph);
add_edge(undigraph, u, v, Weight(3.1));
boost::graph_traits<UndirectedGraph>::edge_descriptor e1, e2;
bool found;
tie(e1, found) = edge(u, v, undigraph);
tie(e2, found) = edge(v, u, undigraph);
std::cout << "in an undirected graph is ";
std::cout << "(u,v) == (v,u) ? " << (e1 == e2) << std::endl;
property_map<UndirectedGraph, edge_weight_t>::type
weight = get(edge_weight, undigraph);
cout << "weight[(u,v)] = " << get(weight, e1) << endl;
cout << "weight[(v,u)] = " << get(weight, e2) << endl;
}
The output is:
in a directed graph is (u,v) == (v,u) ? 0 weight[(u,v)] = 1.2 weight[(v,u)] = 2.4 in an undirected graph is (u,v) == (v,u) ? 1 weight[(u,v)] = 3.1 weight[(v,u)] = 3.1
| Copyright © 2000-2001 | Jeremy Siek, Indiana University (jsiek@osl.iu.edu) |