 |

This chapter is meant as a refresher on elementary graph theory. If the reader has some previous acquaintance with graph algorithms, this chapter should be enough to get started. If the reader has no previous background in graph algorithms we suggest a more thorough introduction such as Introduction to Algorithms by Cormen, Leiserson, and Rivest.
A graph is a mathematical abstraction that is useful for solving many kinds of problems. Fundamentally, a graph consists of a set of vertices, and a set of edges, where an edge is something that connects two vertices in the graph. More precisely, a graph is a pair (V,E), where V is a finite set and E is a binary relation on V. V is called a vertex set whose elements are called vertices. E is a collection of edges, where an edge is a pair (u,v) with u,v in V. In a directed graph, edges are ordered pairs, connecting a source vertex to a target vertex. In an undirected graph edges are unordered pairs and connect the two vertices in both directions, hence in an undirected graph (u,v) and (v,u) are two ways of writing the same edge.
This definition of a graph is vague in certain respects; it does not say what a vertex or edge represents. They could be cities with connecting roads, or web-pages with hyperlinks. These details are left out of the definition of a graph for an important reason; they are not a necessary part of the graph abstraction. By leaving out the details we can construct a theory that is reusable, that can help us solve lots of different kinds of problems.
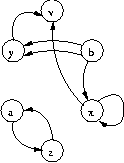
Back to the definition: a graph is a set of vertices and edges. For purposes of demonstration, let us consider a graph where we have labeled the vertices with letters, and we write an edge simply as a pair of letters. Now we can write down an example of a directed graph as follows:
|
V = {v, b, x, z, a, y } E = { (b,y), (b,y), (y,v), (z,a), (x,x), (b,x), (x,v), (a,z) } G = (V, E) |
Figure 1 gives a pictorial view of this graph. The edge (x,x) is called a self-loop. Edges (b,y) and (b,y) are parallel edges, which are allowed in a multigraph (but are normally not allowed in a directed or undirected graph).
Next we have a similar graph, though this time it is undirected. Figure 2 gives the pictorial view.
Self loops are not allowed in undirected graphs. This graph is the undirected version(b,y)), meaning it has
the same vertices and the same edges with their directions removed.
Also the self edge has been removed, and edges such as (a,z)
and (z,a) are collapsed into one edge. One can go the other
way, and make a directed version
of an undirected graph be replacing each edge by two edges, one
pointing in each direction.
Now for some more graph terminology. If some edge (u,v) is in
graph , then vertex v is adjacent to vertex u. In a
directed graph, edge (u,v) is an out-edge of vertex u and an in-edge of vertex v. In an
undirected graph edge (u,v) is incident on vertices u and
v.
In Figure 1,
vertex y is adjacent to vertex b (but b is not
adjacent to y). The edge (b,y) is an out-edge of
b and an in-edge of y. In Figure 2,
y is adjacent to b and vice-versa. The edge
(y,b) is incident on vertices y and b.
In a directed graph, the number of out-edges of a vertex is its out-degree and the number of in-edges
is its in-degree. For an
undirected graph, the number of edges incident to a vertex is its degree. In Figure 1, vertex b has an
out-degree of 3 and an in-degree of zero. In Figure 2, vertex b simply has
a degree of 2.
Now a path is a sequence of edges in a
graph such that the target vertex of each edge is the source vertex of
the next edge in the sequence. If there is a path starting at vertex
u and ending at vertex v we say that v is reachable from u. A path is simple if none of the vertices in
the sequence are repeated. The path <(b,x), (x,v)> is simple,
while the path <(a,z), (z,a)> is not. Also, the path <(a,z),
(z,a)> is called a cycle because the
first and last vertex in the path are the same. A graph with no cycles
is acyclic.
A planar graph is a graph that
can be drawn on a plane without any of the edges crossing over each
other. Such a drawing is called a plane graph. A face of a plane graph is a connected region
of the plane surrounded by edges. An important property of planar
graphs is that the number of faces, edges, and vertices are related
through Euler's formula: |F| - |E| + |V| = 2. This means that a
simple planar graph has at most O(|V|) edges.
The primary property of a graph to consider when deciding which data
structure to use is sparsity, the number of edges relative to
the number of vertices in the graph. A graph where E is close
to V2 is a dense graph, whereas a graph
where E = alpha V and alpha is much smaller than
V is a sparse graph. For dense graphs, the
adjacency-matrix representation is usually the best choice,
whereas for sparse graphs the adjacency-list representation is
a better choice. Also the edge-list representation is a space
efficient choice for sparse graphs that is appropriate in some
situations.
An adjacency-matrix representation of a graph is a 2-dimensional V
x V array. Each element in the array auv stores
a Boolean value saying whether the edge (u,v) is in the graph.
Figure 3 depicts an adjacency matrix for
the graph in Figure 1 (minus the
parallel edge (b,y)). The ammount of space required to store
an adjacency-matrix is O(V2). Any edge can be
accessed, added, or removed in O(1) time. To add or remove a
vertex requires reallocating and copying the whole graph, an
O(V2) operation. The adjacency_matrix class
implements the BGL graph interface in terms of the adjacency-matrix
data-structure.
An adjacency-list representation of a graph stores an out-edge
sequence for each vertex. For sparse graphs this saves space since
only O(V + E) memory is required. In addition, the out-edges
for each vertex can be accessed more efficiently. Edge insertion is
O(1), though accessing any given edge is O(alpha), where
alpha is the sparsity factor of the matrix (which is equal to
the maximum number of out-edges for any vertex in the graph). Figure 4 depicts an
adjacency-list representation of the graph in Figure 1. The
adjacency_list class is
an implementation of the adjacency-list representation.
An edge-list representation of a graph is simply a sequence of edges,
where each edge is represented as a pair of vertex ID's. The memory
required is only O(E). Edge insertion is typically O(1),
though accessing a particular edge is O(E) (not efficient). Figure 5 shows an
edge-list representation of the graph in Figure 1. The
edge_list adaptor class can be
used to create implementations of the edge-list representation.
Tree edges are edges in the search tree (or forest) constructed
(implicitly or explicitly) by running a graph search algorithm over a
graph. An edge (u,v) is a tree edge if v was first
discovered while exploring (corresponding to the visitor explore() method)
edge (u,v). Back edges connect vertices to their
ancestors in a search tree. So for edge (u,v) the vertex
v must be the ancestor of vertex u. Self loops are
considered to be back edges. Forward edges are non-tree edges
(u,v) that connect a vertex u to a descendant v
in a search tree. Cross edges are edges that do not fall into
the above three categories.
Breadth-first search is a traversal through a graph that touches all
of the vertices reachable from a particular source vertex. In
addition, the order of the traversal is such that the algorithm will
explore all of the neighbors of a vertex before proceeding on to the
neighbors of its neighbors. One way to think of breadth-first search
is that it expands like a wave emanating from a stone dropped into a
pool of water. Vertices in the same ``wave'' are the same distance
from the source vertex. A vertex is discovered the first time
it is encountered by the algorithm. A vertex is finished after
all of its neighbors are explored. Here's an example to help make this
clear. A graph is shown in Figure 6 and the
BFS discovery and finish order for the vertices is shown below.
We start at vertex s, and first visit r and w (the two
neighbors of s). Once both neighbors of are visited, we visit the
neighbor of r (vertex v), then the neighbors of w
(the discovery order between r and w does not matter)
which are t and x. Finally we visit the neighbors of
t and x, which are u and y.
For the algorithm to keep track of where it is in the graph, and which
vertex to visit next, BFS needs to color the vertices (see the section
on Property Maps
for more details about attaching properties to graphs). The place to
put the color can either be inside the graph, or it can be passed into
the algorithm as an argument.
A depth first search (DFS) visits all the vertices in a graph. When
choosing which edge to explore next, this algorithm always chooses to
go ``deeper'' into the graph. That is, it will pick the next adjacent
unvisited vertex until reaching a vertex that has no unvisited
adjacent vertices. The algorithm will then backtrack to the previous
vertex and continue along any as-yet unexplored edges from that
vertex. After DFS has visited all the reachable vertices from a
particular source vertex, it chooses one of the remaining undiscovered
vertices and continues the search. This process creates a set of
depth-first trees which together form the depth-first
forest. A depth-first search categorizes the edges in the graph
into three categories: tree-edges, back-edges, and forward or
cross-edges (it does not specify which). There are typically many
valid depth-first forests for a given graph, and therefore many
different (and equally valid) ways to categorize the edges.
One interesting property of depth-first search is that the discover
and finish times for each vertex form a parenthesis structure. If we
use an open-parenthesis when a vertex is discovered, and a
close-parenthesis when a vertex is finished, then the result is a
properly nested set of parenthesis. Figure 7 shows
DFS applied to an undirected graph, with the edges labeled in the
order they were explored. Below we list the vertices of the graph
ordered by discover and finish time, as well as show the parenthesis structure. DFS is used as the kernel for several other graph
algorithms, including topological sort and two of the connected
component algorithms. It can also be used to detect cycles (see the Cylic Dependencies
section of the File Dependency Example).
The minimum-spanning-tree problem is defined as follows: find
an acyclic subset T of E that connects all of the vertices
in the graph and whose total weight is minimized, where the
total weight is given by
One of the classic problems in graph theory is to find the shortest
path between two vertices in a graph. Formally, a path is a
sequence of vertices <v0,v1,...,vk>
in a graph G = (V, E) such that each vertex is connected to the
next vertex in the sequence (the edges
(vi,vi+1) for i=0,1,...,k-1 are in
the edge set E). In the shortest-path problem, each edge is
given a real-valued weight. We can therefore talk about the weight
of a path
There are several variants of the shortest path problem. Above we
defined the single-pair problem, but there is also the
single-source problem (all shortest paths from one vertex to
every other vertex in the graph), the equivalent
single-destination problem, and the all-pairs problem.
It turns out that there are no algorithms for solving the single-pair
problem that are asymptotically faster than algorithms that solve the
single-source problem.
A shortest-paths tree rooted at vertex in graph G=(V,E)
is a directed subgraph
A flow network is a directed graph G=(V,E) with a
source vertex s and a sink vertex
t. Each edge has a positive real valued capacity
function c and there is a flow function f
defined over every vertex pair. The flow function must satisfy three
contraints:
f(u,v) <= c(u,v) for all (u,v) in V x V (Capacity constraint)
The flow of the network is the net flow entering the
sink vertex t (which is equal to the net flow leaving the
source vertex s).
|f| = sumu in V f(u,t) = sumv in V f(s,v)
The residual capacity of an edge is r(u,v) = c(u,v) -
f(u,v). The edges with r(u,v) > 0 are residual edges
Ef which induce the residual graph Gf
= (V, Ef). An edge with r(u,v) = 0 is
saturated.
The maximum flow problem is to determine the maximum
possible value for |f| and the corresponding flow values for
every vertex pair in the graph.
A flow network is shown in Figure
8. Vertex A is the source vertex and H is the target
vertex.
There is a long history of algorithms for solving the maximum flow
problem, with the first algorithm due to Ford and Fulkerson. The
best general purpose algorithm to date is the push-relabel algorithm
of Goldberg
which is based on the notion of a preflow introduced by
Karzanov.
Given an undirected graph G = (V, E), a cut of G is a partition of the vertices into two, non-empty sets X and When the weight of a cut The cut {{0, 6}, {3, 2, 7, 1, 5, 4}} has weight 13:
And the min-cut is {{0, 1, 4, 5}, {2, 3, 6, 7}} (weight 4):
Unlike this example, a graph will sometimes have multiple min-cuts, all of equal weight. A minimum cut algorithm determines one of them as well as the min-cut weight.
Given a directed graph G = (V, E), a cut of G is a partition of the vertices into two, non-empty sets S and T where S is known as the set of source vertices and T is known as the set of sink vertices. The capacity of a cut C = (S, T) is the number of edges from a vertex in S to a vertex in T if G is unweighted, or the sum of weights of edges from a vertex in S to a vertex in T if G is weighted.
When the capacity of a cut C = (S, T) of a directed graph is minimal (that is, no other cut of G has lesser capacity), then C is known as a minimum cut or min-cut.
For example, given this directed graph:
A min-cut is:
where S = {0}, T = {1, 2, 3}, and the min-cut capacity is 1.
V = {v, b, x, z, a, y }
E = { (b,y), (y,v), (z,a), (b,x), (x,v) }
G = (V, E)
Graph Data Structures
Adjacency Matrix Representation
Adjacency List Representation
Edge List Representation
Graph Algorithms
Graph Search Algorithms
Breadth-First Search
order of discovery: s r w v t x u y
order of finish: s r w v t x u y
Depth-First Search
order of discovery: a b e d c f g h i
order of finish: d f c e b a
parenthesis: (a (b (e (d d) (c (f f) c) e) b) a) (g (h (i i) h) g)
Minimum Spanning Tree Problem
T is called the spanning tree.
Shortest-Paths Algorithms
The shortest path weight from vertex u to v is then
delta (u,v) = infinity otherwise.
A shortest path is any path who's path weight is equal to the
shortest path weight.
Network Flow Algorithms
f(u,v) = - f(v,u) for all (u,v) in V x V (Skew symmetry)
sumv in V f(u,v) = 0 for all u in V - {s,t} (Flow conservation)
Minimum Cut Algorithms
Undirected Graphs
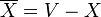 . The weight of a cut is defined as the number of edges between sets X and
. The weight of a cut is defined as the number of edges between sets X and 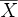 if G is unweighted, or the sum of the weights of all edges between sets X and
if G is unweighted, or the sum of the weights of all edges between sets X and 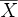 if G is weighted (each edge has an associated, non-negative weight).
if G is weighted (each edge has an associated, non-negative weight).
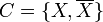 is minimal for a graph G (that is, no other cut of G has a lesser weight), then the cut is known as a minimum cut or a min-cut. For example, given this weighted graph:
is minimal for a graph G (that is, no other cut of G has a lesser weight), then the cut is known as a minimum cut or a min-cut. For example, given this weighted graph:
Directed Graphs
Copyright © 2000-2001
Jeremy Siek, Indiana University (jsiek@osl.iu.edu)