|
Home | Libraries | People | FAQ | More |
boost::accumulators::impl::peaks_over_threshold_impl — Peaks over Threshold Method for Quantile and Tail Mean Estimation.
// In header: <boost/accumulators/statistics/peaks_over_threshold.hpp> template<typename Sample, typename LeftRight> struct peaks_over_threshold_impl { // types typedef numeric::functional::average< Sample, std::size_t >::result_type float_type; typedef boost::tuple< float_type, float_type, float_type > result_type; typedef mpl::int_< is_same< LeftRight, left >::value?-1:1 > sign; // construct/copy/destruct template<typename Args> peaks_over_threshold_impl(Args const &); // public member functions template<typename Args> void operator()(Args const &); template<typename Args> result_type result(Args const &) const; };
According to the theorem of Pickands-Balkema-de Haan, the distribution function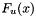 
of the excesses 
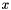over some sufficiently high threshold 
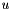of a distribution function 
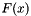may be approximated by a generalized Pareto distribution
with suitable parameters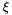 
and 
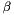that can be estimated, e.g., with the method of moments, cf. Hosking and Wallis (1987),
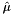and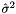 
being the empirical mean and variance of the samples over the threshold 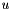. Equivalently, the distribution function 
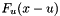of the exceedances 
can be approximated by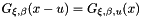 
. Since for 
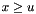the distribution function 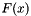can be written as
and the probability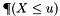 
can be approximated by the empirical distribution function 
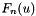evaluated at 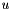, an estimator of 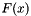is given by
It can be shown that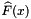 
is a generalized Pareto distribution 
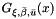with 
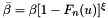and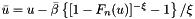 
. By inverting 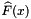, one obtains an estimator for the 
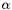-quantile,
and similarly an estimator for the (coherent) tail mean,
cf. McNeil and Frey (2000).
Note that in case extreme values of the left tail are fitted, the distribution is mirrored with respect to the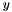 
axis such that the left tail can be treated as a right tail. The computed fit parameters thus define the Pareto distribution that fits the mirrored left tail. When quantities like a quantile or a tail mean are computed using the fit parameters obtained from the mirrored data, the result is mirrored back, yielding the correct result.
For further details, see
J. R. M. Hosking and J. R. Wallis, Parameter and quantile estimation for the generalized Pareto distribution, Technometrics, Volume 29, 1987, p. 339-349
A. J. McNeil and R. Frey, Estimation of Tail-Related Risk Measures for Heteroscedastic Financial Time Series: an Extreme Value Approach, Journal of Empirical Finance, Volume 7, 2000, p. 271-300
